Looking at an algorithm to explore properties of the number puzzle from the TV gameshow “Countdown”. In designing an algorithm we look at various algorithmic and implementation optimisations that reduce the runtime from a minute to just a couple of seconds when searching the problem space.

Background

Countdown is a long-running British TV gameshow based on the French series Des chiffres et des lettres. Contestants complete a number of 30 second word and number puzzles.

In the numbers rounds, a random number generator produces a three-digit number in the range [100, 999]. Given 6 number cards, the aim is to reach the goal number using only standard arithmetic operations: addition, subtraction, multiplication and division. Concatenation of number cards is not permitted. The 6 cards are chosen from a shuffled collection of 24 cards:

\[\{1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10, 25, 50, 75, 100\}\]

A countdown game in progress

Each number card may be used at most once. The intermediate results of all sub-calculations and subexpressions are required to be positive, whole numbers. In the image above, 561 could be obtained from the tiles by \((6+1) \times 8 \times 10 + (9 / 9) = 561\)

The Puzzle

The original puzzle takes a three digit number, and attempts to find an expression, or a combination of the tiles and arithmetic operators, that can produce this number. We’ll look at a related problem:

(1) Of all combinations of 6 tiles from the set, which combination is the most versatile?

(2) Can any combination produce all the values in the range [100, 999]?

This involves generating all expressions from a single card set and seeing how many unique results can be made. Then, repeating the process with every combination of 6 cards.

The algorithm is implemented later written in Java.

Generating Results of All Expressions

Some attempts address the problem by using alternative math notation to simplify generating all expressions([1][2][3][4]). Postfix, or RPN (Reverse Polish Notation) expressions do not require parentheses – the expression above could be written 561 = 6 1 + 8 * 10 * 9 9 / +, for example. Numbers and intermediate results are pushed to a stack, with binary operators working on the top two elements on the stack and pushing a single result.

RPN can be nice as it makes parentheses unnecessary. In some ways it can be easier to enumerate all different possible expressions. However a different approach is used here, by recursively computing the results of all expressions by looking at the ways a card group can be partitioned to form subexpressions on either side of an infix binary operator (\(+, -, \times, /\)):

FUNCTION compute(cards: CardGroup) RETURNS Set of Int
    IF cards.size = 1 THEN
        RETURN { cards[0] }

    result := {}

    FOR partition ∈ every unique* partitioning of cards in 2 groups LOOP
        left := compute(partition.left)
        right := compute(partition.right)
        result := result ∪ combine(left, right)        

    RETURN result

Base case: when we have one card, the only result we can obtain is the value of the card itself.

Otherwise: we look at all the different ways we could place cards on either side of some binary operator by partitioning into 2 groups. Some examples:

cards = \(\require{cancel}\{1,2\}\), the possibilities to go on the left and right are \((\{1\}, \{2\})\) and \(\cancel{(\{2\}, \{1\})}\)
cards = \(\{1,2,3\}\) the possibilities allocating cards either side of this operator are:
- \((\{1\}, \{2, 3\}), (\{2\}, \{1,3\}), (\{3\}, \{1,2\}), \cancel{(\{1,2\}, \{3\}), (\{1,3\}, \{2\}), (\{2,3\}, \{1\})}\).
We recursively call compute to find the result set of all possible subexpressions using the cards appearing on the left and right side of this operator.
each result from both sets are combined using every operator, with invalid intermediate results filtered out.

Combining Results from Subexpressions

For each integer in the left set, we wish to use every operator to combine with each element in the right set, with invalid intermediate results filtered out. An optimisation is made such that this function is commutative – such that \(combine(a, b)=combine(b, a)\) for both two integers and two sets of integers. This means we do not need to compute partitions where the left and right set are only swapped (see crossed-through groups above).

Addition and multiplication are already commutative (always \(a + b = b + a\)). Subtraction and division are not (not always \(a-b\neq b-a\)), but as per the rules intermediate calculations must be positive and whole. So at most one unique result for each operator is possible.

a and b are also included in the result set as if no operator was applied – this has a cumulative effect of not necessarily using all cards in a calculation. Below is the pseudocode for combining two integers, which is applied to every integer pair in the cartesian product of the left and right sets.

FUNCTION combine(a: Int, b: Int) RETURNS Set of Int
    result := {a, b, a+b, a*b}

    hi := max(a, b)
    lo := min(a, b)

    IF a /= b THEN
        result := result ∪ {hi - lo}

    IF hi MOD lo = 0 THEN
        result := result ∪ {hi / lo}

    RETURN result
    
    
FUNCTION combine(left: Set of Int, right: Set of Int) RETURNS Set of Int
    result := {}
    FOR l ∈ left LOOP
        FOR r ∈ right LOOP
            result := result ∪ combine(l, r)
    
    RETURN result

Further Optimisations

Besides commutatitivity of combine we can optimise the algorithm by:

we use a set to keep only unique intermediate subexpression results. This prevents unnecessary computation when the same result is reached by different calculations.
we can use dynamic programming on compute() to store subexpression results for a subgroup of cards, so that they can be resused later. This is also helpful on a larger scale when evaluating multiple combinations of cards possibilities (i.e. the results from subgroup {1, 2, 3, 4, 5} can be used when looking at both complete groups {1, 2, 3, 4, 5, 6} and {1, 2, 3, 4, 5, 7}).

The implementation is optimised by:

optimising the set data structure. Assuming smaller numbers will be generated more frequently, For numbers below a certain threshold, a BitSet is used and larger numbers make use of a Java HashSet. The complexity for lookup/insertion is O(1), though for a BitSet memory space is traded off (for small sets) for a smaller constant time.
exploiting multithreading to compute the results of different CardGroups in parallel.

Results Summary

The answer is yes! 1226/13242 (9.3%) of the possible groups of 6 from the full 24 cards can produce all results in the interval 100-999. The first combination to achieve this is {1, 2, 3, 10, 75, 100}, the last, {8, 9, 9, 10, 25, 75}. There is only 1 combination that is unable to make any values in this range – which is {1, 1, 2, 2, 3, 3}.

Most combinations are able to make far more values outside this range. The most versatile card group is {5, 8, 9, 50, 75, 100} which can make 25913 different values.

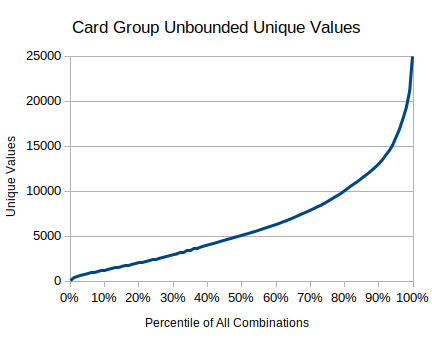
Number of Expressions

Looking at the total number of expressions that can be formed with exactly N cards, or at most N cards. Ignoring some of the constraints and optimisations of the problem (not constricted to [101..999] range, equivalent expressions such as a+b and b+a considered separate, subresults may be non-integer or negative):

Exactly N cards for \(N >= 1\)	At most N cards for \(N >= 1\)
\(1, 8, 192, 7680, 430080, 30965760, ...\)	\(1, 10, 219, 8500, 470485, 33665406, ...\)
\(F(n) = 4^{n-1} \times n! \times Catalan(n-1)\)	??
OEIS A052734

Unique and Valid Results

Of these expressions, only a subset are valid in the context of the problem (all subexpressions are integer and positive), and produce a unique value. Focusing on when expressions consist of exactly N cards, we compute the mean valid and valid & unique results from computing on every unique combination of N cards from the original set of 24.

The number of valid & unique values is several orders of magnitude smaller than all possible expressions. The proportion of valid & unique results of all expressions decreases with larger N. Note that while the total number of expressions is fixed, the valid & unique results obtained will vary depending on the values in the original card set.

Evaluating Optimisations

Looking specifically at the case in chosing 6 cards of the 24, we look at the average runtime of 5 runs of different optimisations. Base is an implementation using the Java HashMap to store the result set:

Exploring the runtime of different optimisation strategies.
DS = optimised set data structure, DP = dynamic programming, 8T = 8 threads (cold start)

Applying dynamic programming to the compute function brings the most benefit – reducing runtime from by 64% (62.2 to 22.2s). Combined with a more efficient IntSet implementation (DP+DS), we get a runtime improvement of 90%. The final variant additionally employing multithreading decrases runtime by 97% from the original baseline.

Closer Look at Multithreading

The DP+S algorithm is executed in parallel as descried above. The benchmarking test meant that the ForkJoinPool was already ‘warm’ – in the results below, a 0.5s penalty (representing startup time) was added to the data to generate the cold dataset. This startup time makes a large proportion of the runtime as the task completes fairly quickly. For longer running tasks (e.g. testing more combinations), one would expect the performance to tend more towards the warmer runtime & speedup, as startup becomes less significant.

The results show linear speedup until 3 threads, where we start to see diminishing returns. I’m curious if this could be improved by changing the order of the search. There could be some cases where a thread is unnecessarily evaluating a card group, before another thread has been able to place its result in the memoised cache.

Some Thoughts & Extensions

SIMD Operations (SIMD) the combine operation processes many* incoming values. Every value from one set needs to be applied with an operator with every value from the other set. There is an opportunity here to use SIMD (Single Instruction Multiple Data) instrcutions on a supported CPU. This would allow for the efficient application of a value from one set to a vector of values in the second set. The incubating Java Vector API could be interesting to try out.
Early Return (ER) the algorithm currently returns all possible results. If we are only interested in whether we can reach all values in a range [101..999], then we could return early and cull a portion of the search if we notice we have hit all values in the interval. A quick attempt at implementing this didn’t seem to reduce runtime significantly. Perhaps the overhead of performing the check does not overcome the benefit of returning early.
More Cards, N > 6 would require some modification to use the long type as the max value with 7 cards is \(100 \times 75 \times 50 \times 25 \times 10^2 \times 9 = 8,437,500,000\) which overflows a Java int (max = \(2,147,483,647\)).

References

[1] Richard Harris – The Model Student: A Game of Six Integers (Part 2)

[2] DataGenetics – Countdown Game Show

[3] YouTube – Graham Hutton/FP 13 The Countdown Problem

[4] YouTube – ComputerPhile/Brute Forcing the Countdown Numbers Game