Puzzle: The Wedding Ring
Looking at solving a combinatorics problem by enumerating all possibilities and analysing to make a generalised solution.
The Puzzle
In certain parts of rural Russia, a would-be bride would gather six long pieces of straw or grass and grasp them in her hand. She then would randomly tie pairs of knots on the top and the bottom. Since there are six blades of grass sticking out above and below the hand, she will tie three knots on the top and three knots on the bottom. The story goes, that if she formed one big ring, she would get married soon. What is the probability that she will get married?
Found as puzzle #3 here, originally as NY Times Numberplay Puzzle from some unknown textbook.

Solving by Enumerating Possibilities
The probability is the number of possibilities of knots that form a loop divided by all the ways the top and bottom ends could be knotted: \(\require{cancel}\)
\[\frac{\text{ways that loop}}{\text{all ways of knotting}}\]Looking at just one end, say there are \(n\) ways of making 3 knots. For the other end, there would also be \(n\) ways of making 3 knots. For every top way of knotting, we could try every bottom way of knotting: so this would give a total of \(n^2\) ways both ends could be knotted:
\[= \frac{\text{ways that loop}}{(\text{ways of knotting one end})^2}\]For each way we knot one end, there are a fixed number of ways we could “match” or knot the other end to make a complete loop:
\[= \frac{\cancel{(\text{ways of knotting one end})} \times {(\text{ways to match an end})}}{(\text{ways of knotting one end})\cancel{^2}} = \frac{\text{ways to match an end}}{\text{ways of knotting one end}}\]Ways of knotting one end there are \(15\) ways we could knot an end together. Assign a number to each blade of grass and look at the unique ways we could pair the numbers together (each pair is a knot).
12 34 56 13 24 56 14 23 56 15 23 46 16 23 45
12 35 46 13 25 46 14 25 36 15 24 36 16 24 35
12 36 45 13 26 45 14 26 35 15 26 34 16 25 34
Ways to match an end for each way the top is knotted, there are \(8\) ways the bottom could be knotted to form a loop:
Top: 12 34 56 Bottom: 23 45 16
23 46 15
24 35 16
24 36 15
25 36 14
25 46 13
26 35 14
26 45 13
...
Result putting it all together:
\[\frac{\text{ways to match an end}}{\text{ways of knotting one end}} = \frac{8}{15} = 53.3\%.\]Analysis & Generalising
Let \(k(2n)\) and \(m(2n)\) be the number of ways we can knot and match an end respectively with \(2n\) blades of grass. Also let \(p(2n)\) be the probability of creating a loop where \(p(2n)=k(2n)/m(2n)\) (as above).
If we have \(2\) blades of grass, \(k(2)=m(2)=1\) (there is only \(1\) way of knotting and matching an end).
Knotting one end Look at any \(2n\) blades of grass. We can choose to knot a single blade of grass with \((2n-1)\) other blades of grass (exclude this blade as it cannot knot to itself). That leaves \((2n-2)\) other unpaired blades of grass which can be paired. The \((2n-1)\) possibilities for a single join is multiplied by all the possibilities of joining the remaining \((2n-2)\) blades of grass:
\[k(2n) = (2n-1)\times k(2n-2)\] \[k(2n) = (2n-1)\times (2n-3) \times (2n-5) \times ...\] \[k(2n) = (2n-1)!!\]Where \(k!!\) is the double factorial – the product of all numbers with the same parity as k up to and including k (i.e. all odd numbers or all even numbers up to/including k).
Matching other end To create a full loop with already knotted top ends, at each step there are \((2n-2)\) possibilities to create a bottom knot – we have to exclude the current blade and also the starting blade until all others are first joined. Each knot leaves \((2n-2)\) unjoined blades of grass. The possibilities for a single join are multiplied by the possibilities of joining all remaining blades of grass.
\[m(2n) = (2n-2)\times m(2n-2)\] \[m(2n) = (2n-2)\times (2n-4)\times (2n-6)\times ...\] \[m(2n) = (2n-2)!!\]Probability using the above definitions:
\[p(2n) = \frac{(2n-2)!!}{(2n-1)!!}\]or “all the even numbers up to/not including the number of blades of grass divided by all the odd numbers up to/not including the number of blades of grass”.
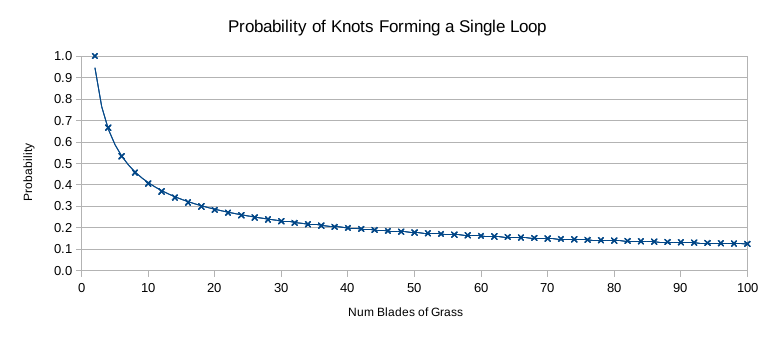
Computing Some Values for Larger Numbers
2n Knotting: (2n-2)!! Matching: (2n-1)!! Probability
2 1 1 1/1 1.000
4 2 3 2/3 0.667
6 8 15 8/15 0.533
8 48 105 16/35 0.457
10 384 945 128/315 0.406
12 3840 10395 256/693 0.369
14 46080 135135 1024/3003 0.341
16 645120 2027025 2048/6435 0.318
18 10321920 34459425 32768/109395 0.300