Puzzle: Troll Passage
Exploring and generalising an optimisation puzzle using calculus.
The Puzzle
Every day you make a trip from A to B, 2 miles away. But your trip is unpredictable. On 50% of the days, you can walk between A and B without any obstruction.
The other 50% of the time, a troll appears at the halfway point, blocking your trip. The troll also activates an invisible barrier that blocks 1 mile perpendicularly in both directions, forcing you to walk around it to complete your trip. You cannot see the troll or the barrier until you are halfway from A to B, so you cannot plan in advance whether you need to walk around the barrier. You do know the troll appears randomly 50% of the time.
If you can walk in straight lines to any points between A and B, what is your best strategy so you walk the least distance on average? What is that distance?
Puzzle as described in 5. Avoiding the Troll / Mr Barton Maths. Also described and solved on Mind your Decisions / Sunday Puzzle.
(1) Solving the Puzzle
Paths to and from the potential barrier We need to walk to some point where the troll would setup the barrier, before we know if the toll is there or not. This point will be anywhere perpendicular to the direct path, passing through the midpoint. Let’s call \(d\) the distance from the original path where we encounter the troll.
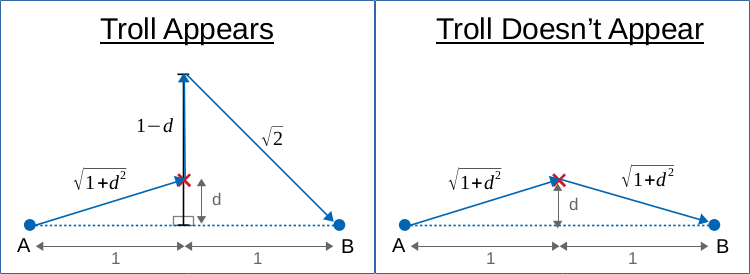
| Troll Appears | No Troll | |
|---|---|---|
| Walking to d | \(\sqrt {1+d^2}\) | \(\sqrt {1+d^2}\) |
| Walking around the barrier | \(+ (1-d)\) | |
| Shortest path to B | \(+ \sqrt 2\) (from end of barrier) | \(+ \sqrt {1+d^2}\) (from d) |
| Total | \(=\sqrt {1 + d^2} + 1 - d + \sqrt 2\) | \(2\sqrt {1+d^2}\) |
Expected Walk Length The average of the two walks gives the expected distance, as it is equally likely the troll will or won’t appear. We’ll use \(E(d)\) to describe the expected distance travelled, given a certain deviation \(d\) from the direct path.
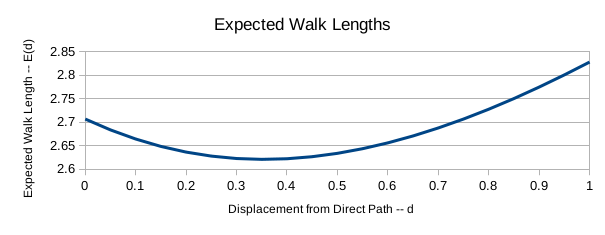
\[E(d) = \frac{1}{2}(\sqrt{1+d^2} + 1 - d + \sqrt{2}) + \frac{1}{2}(2\sqrt {1 + d^2})\] \[E(d) = \frac{1}{2} (3 \sqrt{1+d^2} + 1 - d + \sqrt2)\]Minimising Expected Distance Traveled Plotting the function \(E(d)\) shows that the minimum expected distance is \(E(d) \approx 2.62\). This is possible if we aim to meet the troll at a displacement of \(d\approx 0.35\) from the direct path from A to B:
To find an exact solution, we can use calculus. First, find the derivative of \(E(d)\) and solve for when \(E'(d) = 0\):
\[E(d) = \frac{3}{2} \sqrt{1+d^2} + \frac{1}{2} - \frac{d}{2} + \frac{\sqrt2}{2}\] \[E^\prime (d) = \frac{3d}{2\sqrt {1 + d^2}} - \frac{1}{2}\]\(E^\prime (d)\) is at a minimum when \(E^\prime (d) = 0\):
\[\frac{3d}{2\sqrt {1 + d^2}} - \frac{1}{2} = 0\] \[d = \frac{\sqrt{2}}{4}\]This gives an answer for the minimum at \((0.35, 2.62)\) (2 dp).
(2) Exploring Minimal Expected Walk Length for Different p
Previously, the troll appeared with probability \(p=0.5\) – it was equally likely to appear as not appear. It could be interesting to look at the strategy to minimise the expected distance for different probabilities of the troll appearing. Use \(E(p,d)\) to describe the expected walk langth given a probability of appearing, and deviation from the path:
\[E(p, d) = p(\sqrt{1+d^2} + 1 - d + \sqrt{2}) + (1-p)(2\sqrt {1 + d^2})\] \[E(p, d) = (2 - p) (\sqrt {1 + d^2}) + p(1+\sqrt{2} - d)\]Minimising to minimise the function, we can calculate the partial derivative of E with respect to d.
\[\frac{ \delta E } { \delta d} = \frac{d(2-p)}{\sqrt{1 + d^2}} - p\]\(d\) is at a minimum when \(\frac{ \delta E } { \delta d} = 0\):
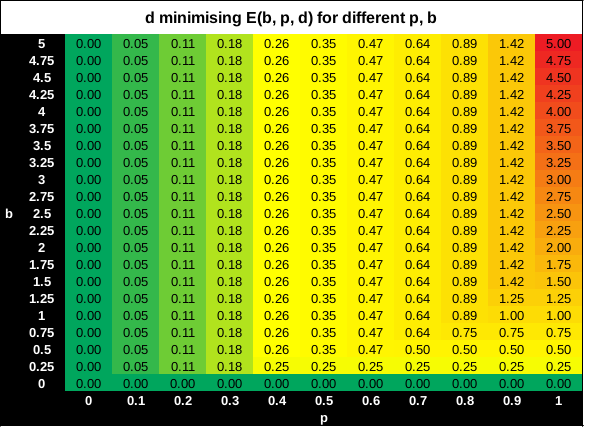
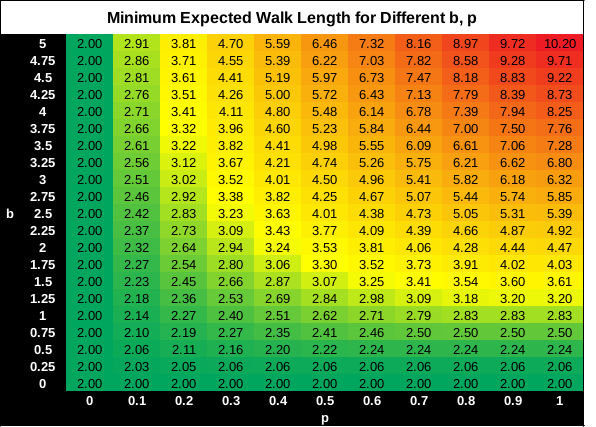
\[\frac{ \delta E } { \delta d} = 0\] \[d = \frac{p}{2\sqrt{1-p}}\]A heatmap of \(E(p, d)\) for different \(p\) and \(d\). The curve overlay shows \(d\) minimising \(E(p, d)\) for different \(p\):
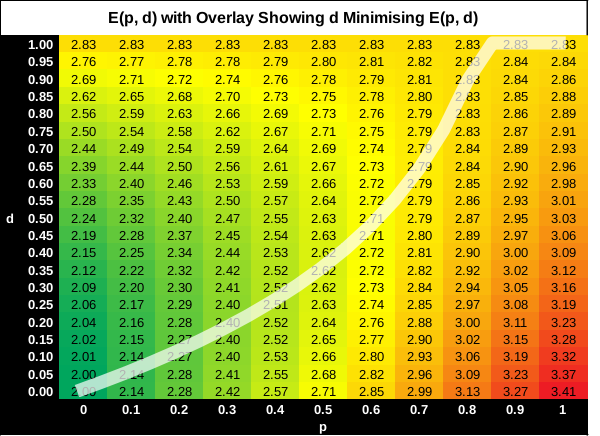
(3) Exploring Minimal Expected Walk Length for Different Barrier Sizes
Say the troll sets up a barrier with size \(b\) and \(d \le b\). How would this affect the strategy? Using a similar formula for the expected walk length, and partial derivative with respect to \(d\):
\[E(b, p, d) = p(\sqrt{1+d^2} + (b - d) + \sqrt{1 + b^2}) + (1-p)(2 \sqrt{1+d^2})\] \[\frac{\delta E}{\delta d} = \frac{d(2-p)}{\sqrt{1 + d^2}} - p\]Notice that the partial derivative does not involve b and is the same as that found in part (2). So this can be solved in the same way, with the additional constraint that \(d \le b\):
\[d = min(b, \frac{p}{2\sqrt{1-p}})\]