Calculating Square Roots by Hand
For a recent project I needed to be able to compute square roots by hand, without the aid of a calculator. This was something I had never attempted before (at school or otherwise), so went about learning the process for doing it.
This particular algorithm is an iterative process similar to long division that gives an exact solution (if one exists), or is otherwise continued to as many decimal places as desired. There’s a good description of the process and why it works here.
Algorithm & Example
Let’s say we wish to calculate the square root of 54321, to 1 decimal place:
| Step | Example | Description |
|---|---|---|
| 1 | 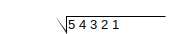 |
Setup the square root |
| 2 | 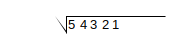 |
From the right to the left, group the digits in pairs. 5 is in a group by itself here. |
| 3 |  |
Find the largest number that when squared is less than or equal to the first group. Here 22 = 4, and 4 is the largest square smaller than or equal to 5. Write the number above, and the square below. |
| 4 | 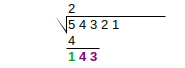 |
Subtract the two numbers and write below. Then, bring down the two digits of the next group. |
| 5 | 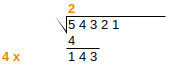 |
Write on the side double the result so far, with x as the last digit |
| 6 | 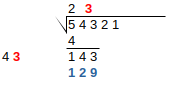 |
We need to find the largest digit for x such that this side number (with x as the last digit), multiplied by x is smaller than or equal to the current remainder. With some experimentation here, we choose 3 as the last digit as 43 * 3 = 129, and 129 <= 143. Add this digit to the result above, and add the multiplication result below |
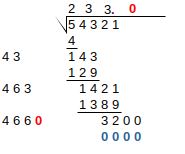
Steps 4-6 are repeated until the exact solution is found, or sufficient precision is achieved. In round 4, if there are no more groups to “bring down”, we instead write zeroes, and introduce a decimal point in the result:
| Step 4 (subtract, down next 2 digits) |
Step 5 (double result so far) |
Step 6 (next digit and multiply) |
|
|---|---|---|---|
| Round 2 | 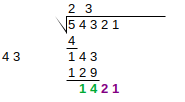 |
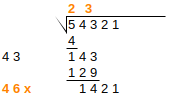 |
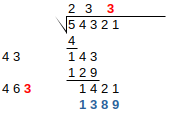 |
| Round 3 | 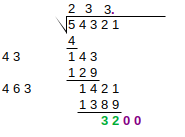 |
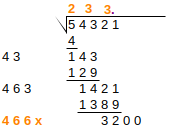 |
 |
| Round 4 | 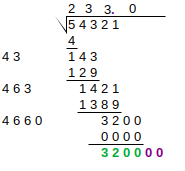 |
 |
 |
We stop here, and can read the result from the top, which is 233.1 to 1 decimal place.
Square Root of 3
This worked example of square root 3 on paper is correct to 17 digits (using the last for rounding). The intermediate calculations get pretty big and cumbersome at this stage. Though this final result actually has a higher precision than calculated in my spreadsheet, due to the limits of the floating point representation it uses behind-the-scenes.
