The Maths of Liu Hui's Pi Algorithm
Liu Hui’s algorithm for approximating pi from 3rd century China is significant as it gave the most accurate valuation for pi in the world for over 1200 years. This looks in more detail at how the result is obtained geometrically and algebraically from first principles. It is an elaboration of the mathematical aspects of the procedure as described in the Wikipedia article.
Theory
The circumference of a circle can be approximated by the perimeter of a regular polygon inscribed within a circle. As the number of sides of the polygon increases, the better the approximation.
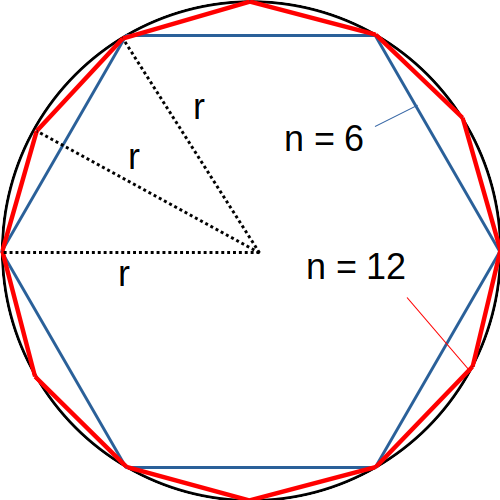
The algorithm is interesting as it calculates from a shape with n-sides, the side-length of a shape with 2n sides with minimal computation. From the side-length, the perimeter of the n-sided-agon can be calcualted, and hence an approximation for the diameter of the circle – used to determine pi. The process can be repeated iteratively to produce closer approximations (i.e, n becomes as large as desired).
A Modern Derivation
The original description of the process with translation can be found in [1].
We look at a circle where \(s_n\) denotes a single side-length of an n-sided regular polygon inscribed in the unit-circle and \(s_{2n}\) the side-length of a polygon with double that number of sides. The goal is to find a formula for \(s_{2n}\) in terms of \(s_{n}\).

3 observations here:
| 1 | \((\frac{s_n}{2})^2 + x^2 = r^2\) | by Pythagoras in blue triangle |
| 2 | \((\frac{s_n}{2})^2 + y^2 = {s_{2n}}^2\) | by Pythagoras in red triangle |
| 3 | \(x+y=r\) | x and y together are the radius |
From these, we can rearrange to state \(s_{2n}\) in terms of \(s_n\)
| 4 | \(x = \sqrt{r^2 - (\frac{s_n}{2})^2}\) | rearrange 1 |
| 5 | \(y=r-x\) | rearrange 3 |
| 6 | \(y = r - \sqrt{r^2 - (\frac{s_n}{2})^2}\) | substitute 4 in 5 |
| 7 | \({s_{2n}}^2 = (\frac{s_n}{2})^2 + \left( r - \sqrt{r^2 - (\frac{s_n}{2})^2} \right) ^2\) | substitute 6 into 2 |
| 8 | \({s_{2n}}^2 = \frac{ {s_n}^2}{4} + \left( r - \sqrt{r^2 - \frac{ {s_n}^2}{4}} \right) ^2\) | expand |
This final formula is roughly equivalent to the calculation used repeatedly in Liu Hui’s description[1] where a circle with radius 10 was used in his calculations. Since the shape is a regular polygon, the perimeter is simply \(n \times s_n\).
\[C = 2\pi r\] \[\pi = C / 2r\] \[C \approx n \times s_n\] \[\pi \approx \frac{n \times s_n}{2r}\]Inequality for Pi
Liu Hui looked at the areas of the shapes to determine an upper and lower bound for the value. Use \(A_n\) to describe the area of a shape with n-sides, and \(D_n\) to describe the difference in area between a shape and a shape with half the number of sides:
| Diagram | Description |
|---|---|
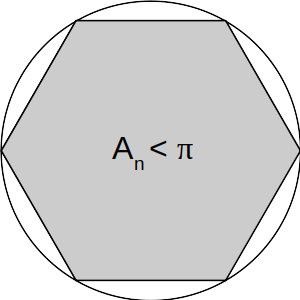 |
The area of an n-sided polygon is smaller than pi |
 |
The area of an 2n-sided polygon is also smaller, but closer to pi |
 |
\(D_{2n}\) is the extra area added when the number of sides was doubled. |
 |
This is also \(D_{2n}\), but with the area distributed/’reflected’ outside the perimeter of 2n-sided shape. |
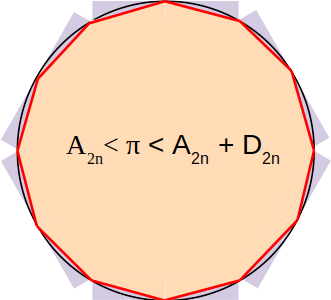 |
\(A_{2n} + D_{2n}\) is bigger the area of the circle |
Hence:
\[A_{2n} < \pi < A_{2n} + D_{2n}\]A Simplified Iterative Algorithm
We can further reduce the number of operations through some algebra[4]. If we are to apply this repeatedly and only interested in the final length, we don’t need to calculate the exact side length (or side length squared) with each iteration. If we assume a unit-circle (r = 1) and starting with (7):
| 9 | \({s_{2n}}^2 = 2 - \sqrt{4 - {s_n}^2}\) | simplify 7 |
| 10 | \(s_{2n} = \sqrt{2 - \sqrt{4 - {s_n}^2}}\) | simplify 9 |
| 11 | \(2 - {s_{2n}}^2 = \sqrt{4 - {s_n}^2}\) | rearrange 10 |
| 12 | let \(k_n = (2 - {s_{n}}^2)\) | |
| 13 | \(k_{2n} = \sqrt{2 + k_n}\) | substitute 12 in 11 |
With each iteration, we can calculate the next \(k_n\), instead of \(s_{n}\). This has the benefit of only requiring two operations now: a single addition followed by a square root.
When we have finished iterating, we are left with some \(k_n\). But from (12) we have \(k_n = (2 - {s_{n}}^2)\). We get the final side length at the end by \({s_n} = \sqrt{2 - k_n}\).
References
[1] Lam Lay-Yong, Circle Measurements in Ancient China
[2] Siu Man-Keung, An Excursion in Ancient Chinese Mathematics
[3] Alexei Volkov, Zhao Youqin and His Calculation of Pi
[4] Wikipedia, Liu Hui’s Pi Algorithm